Question

Find the common ratio & the next three terms in the sequence.

2.-6, 18, -54, ...
a
Common Ratio: r= 3 Next 3 terms: 32, -64, 128
b
Common Ratio: r = 5 Next 3 terms: 1250, 6250, 31250
C
Common Ratio: r = 5 Next 3 terms: 250, 1250, 6250
Common Ratio: r = -B Next B terms: 162, -486, 1458

Answer 1

We conclude that:

• Common ratio: r = -3

• Next three terms: 162, -486, 1458

Hence, option D is correct.

Explanation:

Given the geometric sequence

2, -6, 18, -54, ...

Here:

`a_1=2`

A geometric sequence has a constant difference 'r' and is defined by

`a_n=a_1\cdot \:r^(n-1)`

computing the differences of all the adjacent terms

`(-6)/(2)=-3,\:\quad (18)/(-6)=-3,\:\quad (-54)/(18)=-3`

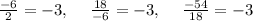
The ratio of all the adjacent terms is the same and equal to

`r=-3`

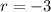
now substituting
`a_1=2` and
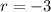`r=-3` in the nth term of the sequence

`a_n=a_1\cdot \:r^(n-1)`

now substituting n = 5 to determine the 5th term

`a_5=2\left(-3\right)^(5-1)`

`a_5=3^4\cdot \:2`

`a_5=2\cdot \:81`

`a_5=162`

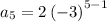
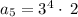
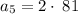
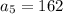
now substituting n = 6 to determine the 6th term

`a_6=2\left(-3\right)^(6-1)`

`a_6=-2\cdot \:243`

`a_6=-486`

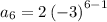
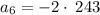
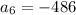
now substituting n = 7 to determine the 7th term

`a_7=2\left(-3\right)^(7-1)`

`a_7=2\cdot \:729`

`a_7=1458`

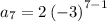
Therefore, we conclude that:

• Common ratio: r = -3

• Next three terms: 162, -486, 1458

Hence, option D is correct.