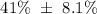ANSWER
Step-by-step explanation
The confidence interval is given as (32.9%, 49.19%)
Firstly, we need to find the value of P and ME
Assume, that the upper limit of the confidence interval is 49.19%, and the lower limit is 32.9%
P + ME = 49.1 ---------- 1
P - ME = 32.9 ------------2
The above equation can be solved simultaneously by using the substitution method
Isolate P in equation 1
P = 49.1 - ME
substitute the value of P = 49.19 - ME into equation 2
49.1 - ME - ME = 32.9
49.1 - 2ME = 32.9
subtract 49.1 from both sides of the equation
49.1 - 49.1 - 2ME = 32.9 - 49.1
-2ME = 32.9 - 49.1
-2ME = -16.2
Divide both sides by -2
-2ME/-2 = -16.2/-2
ME = 8.1
To find P, substitute the value of ME = 8.15 into the equation 1
P = 49.1 - 8.1
P = 41
From the above calculations, you will see that P = 41% and ME = 8.1%
Hence the confidence interval can be expressed as