Question

Which linear function represents the line given by the point-slope equation y – 2 = 4(x – 3)?

A. f(x) = 6x – 1
B. f(x) = 8x – 6
C. f(x) = 4x – 14
D. f(x) = 4x – 10

Answer 1

(D). f(x) = 4x – 10

Explanation:

♥☺

Answer 2

The linear function which represents the line given by the point-slope equation y – 2 = 4(x – 3) will be:

• f(x) = 4x - 10

Hence, option D is correct.

Explanation:

We know that the point-slope form of the line equation

`y-y_1=m\left(x-x_1\right)`

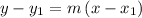
where

• m is the slope of the line

• (x₁, y₁) is the point

Given the equation

y – 2 = 4(x – 3)

comparing with the point-slope form of the line equation, we get

m = 4

(x₁, y₁) = (3, 2)

We also know the slope-intercept form of the line equation

y = mx + b

where m is the slope and b is the y-intercept

since we already fetched m = 4 and (x₁, y₁) = (3, 2)

so substitute m = 4 and (3, 2) in the slope-intercept form of the line equation to determine the y-intercept b

y = mx + b

2 = 4(3) + b

2 = 12 + b

flip the equation

12 + b = 2

subtract 12 from both sides

12 + b - 12 = 2 - 12

b = -10

now substitute b = -10 and m = 4 in the slope-intercept form of the line equation

y = mx + b

y = 4x + (-10)

y = 4x - 10

f(x) = 4x - 10 ∵ y = f(x)

Therefore, the linear function which represents the line given by the point-slope equation y – 2 = 4(x – 3) will be:

• f(x) = 4x - 10

Hence, option D is correct.