Question

Concide the following functions: f (x)=x^2+10x+29. Write function form of

f (x)=a (x-h)^2+k. Where a,h and k are constants. Then find minimum or maximum. Please and thank you.

Answer 1

f(x) = x² + 10x + 29
y = x² + 10x + 29
y - 29 = x² + 10x
y - 29 + 25 = x² + 10x + 25
y - 4 = x² + 5x + 5x + 25
y - 4 = x(x) + x(5) + 5(x) + 5(5)
y - 4 = x(x + 5) + 5(x + 5)
y - 4 = (x + 5)(x + 5)
y - 4 = (x + 5)²
y = (x + 5)² + 4
f(x) = (x + 5)² + 4

Minimum:
`x = (-b)/(2a) = (-10)/(2(1)) = (-10)/(2) = -5`
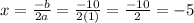
Maximum:
`x = (b)/(-2a) = (10)/(-2(1)) = (10)/(-2) = -5`

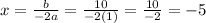
f(x) = (x + 5)² + 4
y = (-5 + 5)² + 4
y = (0)² + 4
y = 0 + 4
y = 4

The local maximum value of the function is located at x = -5.