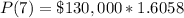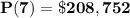Question

15. Annual sales for a surf shop are $130,000

and are increasing at a rate of 7% per year; 7 years
find the Function and the
Value after 7 years

Answer 1

`P(7)=\$208,752`

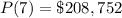
Explanation:

Exponential Growth

The natural growth of some magnitudes can be modeled by the equation:

`P(t)=P_o(1+r)^t`

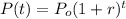
Where P(t) is the actual amount of the magnitude, Po is its initial amount, r is the growth rate and t is the time.

It's given the annual sales for a surf shop are Po=$130,000. They are increasing at a rate of r=7% = 0.07 per year. Substituting values, the function is:

`P(t)=\$130,000(1+0.07)^t`

`\boxed{P(t)=\$130,000(1.07)^t}`

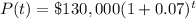
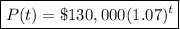
The value of the function after t=7 years is

`P(7)=\$130,000(1.07)^7`

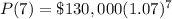
Computing:

`P(7)=\$130,000*1.6058`

`\mathbf{P(7)=\$208,752}`