Question

How many liters of a 10% solution should be mixed with 60 liters of a 25% solution to

get a 15% solution?

Answer 1

120 liters of the 10% solution should be mixed with 60 liters of a 25% solution to get a 15% solution.

Explanation:

Let 'x' be the quantity of 10% solution

Given that we need determine many liters of a 10% solution should be mixed with 60 liters of a 25% solution to get a 15% solution.

As

10% of x = 0.1x

60 liters of a 25% = 60 × 0.25

Thus,

The equation becomes

`0.1x+60* \:0.25=0.15\left(x+60\right)`

Multiply both sides by 100

`0.1x* \:100+15* \:100=0.15\left(x+60\right)* \:100`

`10x+1500=15\left(x+60\right)`

`10x+1500=15x+900`

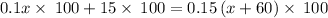
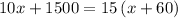
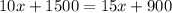
Subtract 1500 from both sides

`10x+1500-1500=15x+900-1500`

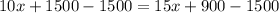
Simplify

`10x=15x-600`

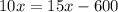
Subtract 15x from both sides

`10x-15x=15x-600-15x`

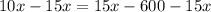
Simplify

`-5x=-600`

Divide both sides by -5

`(-5x)/(-5)=(-600)/(-5)`

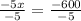
Simplify

`x=120`

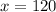
Therefore,

• 120 liters of the 10% solution should be mixed with 60 liters of a 25% solution to get a 15% solution.