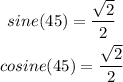Answer:
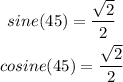
Explanation:
The hypotenuse of a reference triangle that lies on the unit circle is the radius of the unit circle. Therefore, if it has a radius of 3 and a reference triangle of 45 degrees.
Remember that sine and cosine are represented by the following equations:
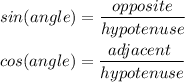
Now, for the following circle and the reference triangle:
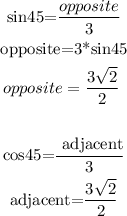
Hence, for the sin and cosine: