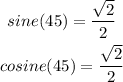Question

6. Given a circle with a radius of 3 and a reference triangle of 45°. What are the sine andcosine of the angle?

Answer 1

`\begin{gathered} sine(45)=(√(2))/(2) \\ cosine(45)=(√(2))/(2) \end{gathered}`

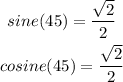
Explanation:

The hypotenuse of a reference triangle that lies on the unit circle is the radius of the unit circle. Therefore, if it has a radius of 3 and a reference triangle of 45 degrees.

Remember that sine and cosine are represented by the following equations:

`\begin{gathered} sin(angle)=(opposite)/(hypotenuse) \\ cos(angle)=\frac{adjacent\text{ }}{hypotenuse} \end{gathered}`

Now, for the following circle and the reference triangle:

`\begin{gathered} \text{ sin\lparen45\rparen=}(opposite)/(3) \\ \text{ opposite=3*sin\lparen45\rparen} \\ opposite=(3√(2))/(2) \\ \\ \text{ cos\lparen45\rparen=}\frac{\text{ adjacent}}{3} \\ \text{ adjacent=}(3√(2))/(2) \end{gathered}`

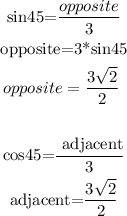
Hence, for the sin and cosine:

`\begin{gathered} sine(45)=(√(2))/(2) \\ cosine(45)=(√(2))/(2) \end{gathered}`