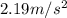The equation to calculate the acceleration due to gravity at a given height is,
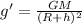
Here, G is the gravitational constant, M is the mass of earth, R is the radius of earth and h is the given height.
Part (a)
The given height is
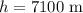
Substitute the known values in equation,
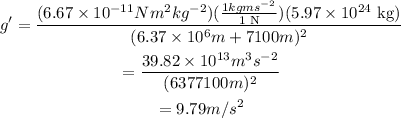
Thus, the effective value of g at the given height is
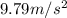
Part (b)
The given height is

Substitute the known values in the same equation,
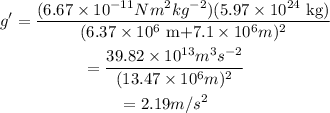
Thus, the effective value of g at the given height is