Question

Brandon Brandon Drew the two congruent squares shown he divided one square into 2 congruent triangular parts he divided the other square into 2 congruent rectangular parts

Answer 1

Incomplete question: Options

(a) Each triangular part and each rectangular part represents 1/2 the area of one square.

(b) Each triangular part has an area that is greater than the area of each rectangular part.

(c) Each triangular part and each rectangular part represents 1/4 the area of one square

(d) Each rectangular part has an area that is greater than the area of each triangular part.

See attachment for squares

Answer:

(a) Each triangular part and each rectangular part represents 1/2 the area of one square.

Explanation:

Given

See attachment

Required

Which statement is true

Before the division, the area of both squares is:

`Area = l * w`

After the division:

The area of the triangle is:

`Area = (1)/(2) * base * height`

`A_1 = (1)/(2) * l * w`

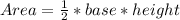
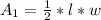
Substitute Area for l * w

`A_1 = (1)/(2) *Area`

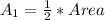
This equals half the area of the square

The area of the rectangle is:

`Area = length * width`

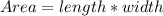
The length of the rectangle is now half the length of the original square.

So, we have:

`A_2 = (1)/(2) l * w`

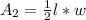
Substitute Area for l * w

`A_2 = (1)/(2) *Area`

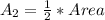
From the values of A1 and A2, we can conclude that (a) is true