Question

Please help with this problem:A rocket is launched vertically from the ground with an initial velocity of 64 ft / sec. (a)Write a quadratic function h(t) that shows the height, in feet, of the rocket t seconds after it was launched.(b)Determine the rocket’s maximum height, the amount of time it took to reach its maximum height, and the amount of time it was in the air. Show work for all steps.(c)Graph h(t) on the coordinate plane using important information from part b.

Answer 1

(a) We are asked to write a quadratic function h(t) that shows the height, in feet, of the rocket t seconds after it was launched.

The initial velocity of the rocket is 64 ft/sec.

Recall from the equations of motion, we have

`s=ut-(1)/(2)at^2`

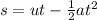
Here s will be replaced by the height h(t), a is the acceleration due to gravity that is 32.17 ft/sec^2 and u is the initial velocity of the rocket.

Plugging the values, the above equation becomes

`\begin{gathered} h(t)=64t-(1)/(2)\cdot32.17\cdot t^2 \\ h(t)=64t-16.085t^2 \end{gathered}`

Therefore, we have got the quadratic equation that shows the height of the rocket t seconds after it was launched.

`h(t)=64t-16.085t^2`

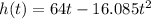
(b) The amount of time it took to reach its maximum is given by the vertex of the quadratic function.

`t=-(b)/(2a)`

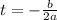
From part (a), the coefficients of the quadratic function are

a = -16.085

b = 64

c = 0

`t=-(64)/(2(-16.085))=1.989\;sec`

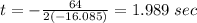
So, it takes 1.989 seconds to reach the maximum height.

The corresponding maximum height of the rocket can be found by plugging t = 1.989 into the quadratic function.

`\begin{gathered} h(t)=64(1.989)-16.085(1.989)^2 \\ h(t)=127.296-63.634 \\ h(t)=63.662 \end{gathered}`

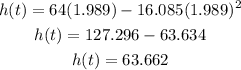
Therefore, the rocket’s maximum height is 63.662 ft

The amount of time the rocket was in the air is double the time to reach the maximum height.

`2*1.989=3.978\;sec`

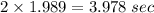
Therefore, the rocket was in the air for 3.978 seconds.

(c) Let us sketch an approximate graph of the function using the information from part (b)