Question

A rectangular box is x feet long and x feet wide. The volume of the box is (4x^8 + 3x^6) cubic ft. What polynomial represents the height of the box in feet?

Answer 1

`h = (4x^(8) + 3x^(6))/(x^(2))`

`h = (4x^(8))/(x^(2)) + (3x^(6))/(x^(2))`

`h = 4x^(6) + 3x^(4)`

Answer 2

Hence, the height, in feet, of the rectangular box is given by the polynomial
`h=4x^6+3x^4`

Explanation:

The volume of a rectangular box is given by the formula:

`V=length*width*height`

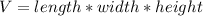
We are given
`V=4x^8+3x^6`, length = x, and width = x , plugging these into the formula and figuring out height:

`V=length*width*height\\4x^8+3x^6=(x)(x)(h)\\4x^8+3x^6=x^2h\\h=(4x^8+3x^6)/(x^2)\\h=(x^2(4x^6+3x^4))/(x^2)\\h=4x^6+3x^4`

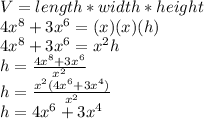
Hence, the height, in feet, of the rectangular box is given by the polynomial
`h=4x^6+3x^4`