Question

The average price of a brand of coffee that you buy is $4.89 for each 11-ounce can. Depending on where you shop, the prices of this can of coffee vary by as much as $1.58. Find the minimum and maximum prices of this coffee.

Answer 1

Minimum price of the coffee = $ 4.1

Maximum price of the coffee = $ 5.68

Explanation:

Let us assume

The minimum price of the coffee = $x

As given , the prices of this can of coffee vary by as much as $1.58.

⇒ Maximum price of the coffee will be = $ x+1.58

Now, as given , The average price of coffee = $4.89

⇒
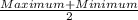`(Maximum + Minimum)/(2)` = $4.89

⇒ Maximum + Minimum = 9.78

⇒x + 1.58 + x = 9.78

⇒2x + 1.58 = 9.78

⇒2x = 9.78 - 1.58

⇒2x = 8.2

⇒x =
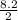`(8.2)/(2)` = 4.1

∴ we get

Minimum price of the coffee = x = $ 4.1

Maximum price of the coffee = x + 1.58 = $ 4.1 + 1.58 = $ 5.68