Question

A 90kg man is standing still on frictionless ice. His friend tosses him a 10kg ball, which has a horizontal velocity of 20m/s. After catching the ball, what is the man's velocity?

Answer 1

Using the conservation of momentum,
ma*va1 + mb*vb1 = ma*va2 + mb*vb2
Let:
ma = mass of the ball
va = velocity of the ball
mb = mass of the man
vb = velocity of the man
The subscript 1 is known as initials while 2 is for finals.
Before the man throws the ball, he starts at rest, meaning the initial velocity of the ball and the initial velocity of the man are zero. So
0 = ma*va2 + mb*vb2
Given ma = 10 kg; va = 20 m/s; mb = 90 kg; vb is unknown, therefore
-(mb*vb2) = ma*va2
vb2 = -(ma*va2)/mb2 = -(10*20)/90 = -2.22 m/s
Notice that his velocity is negative because when he finally throws the ball (say to the right), he moves at the opposite direction (that is to the left) on which he stands on the frictionless surface.

Answer 2

The man's velocity is
`(2.222,0,0)(m)/(s)`

Step-by-step explanation:

If we want to solve this exercise, we need to use the Momentum Conservation Principle.

The momentum is a vectorial magnitude define as :

`p=m.v`

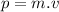
Where ''p'' is the momentum

Where ''m'' is the mass of the object

And where ''v'' is the velocity vector.

For any collision occurring in an isolated system, momentum is conserved. We define an isolated system as a system in which the sumatory of exterior forces is equal to zero.

For this exercise, we can solve it as a collision ⇒

`m1.v1=m2.v2`

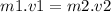
Where ''m1'' is the mass of the ball

Where ''v1'' is the velocity vector of the ball

Where ''m2'' is the mass of the man

And where ''v2'' is the velocity vector of the man after catching the ball.

If we replace all the data in the equation :

`(10kg).(20(m)/(s))=(90kg).v2`

`v2=2.222(m)/(s)`

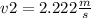
This will be the magnitude of the velocity vector from the man.

If we define as positive the sense in which his friend tosses him the ball (given that we know the direction), the man's velocity will be
`(2.222,0,0)(m)/(s)`