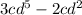Question

Which expression is equivalent to 6c^2d^5/2c - 2c^10/d^-2? The slashes represent a fraction. This is a question on my review that I was using to study for the test I have to school.

Answer 1

The given expression is-

`(6c^2d^5)/(2c)-(2c^(10))/(d^(-2))`

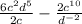
We can solve this using the cross method to subtract the fractions. The following property shows this method.

`(a)/(b)-(c)/(d)=(ad-bc)/(c\cdot d)`

Using this property, we have

`(6c^2d^5d^(-2)-2c^(10)2c)/(2c\cdot d^(-2))`

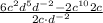
Now, we solve the products.

`(6c^2d^3-4c^(11))/(2cd^(-2))`

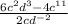
We simplify the terms since all of them can be divide by 2c

`(3cd^3-2c^(10))/(d^(-2))`

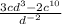
At last, we use the negative exponent property. This property allows us to change the position of the power with negative exponent.

`d^2\cdot(3cd^3-2c^(10))`

At last, we solve this product using the distributive property.

Therefore, the equivalent expression is

`3cd^5-2cd^2`