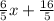Answer:
y =
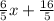
Explanation:
The slope-intercept form is y = mx + b, where "m" is the slope and 'b" is the y-intercept.
Given: G(-6, -4) and E(4, 8)
Now we can use these points G(-6, -4) and E(4, 8) and find the slope.
Slope (m) =

Here x1 = -6, y1 = -4, x2 = 4 and y2 = 8
Plug in these values in the above formula, we get
slope(m) =

=

Slope (m) =

Now we can use the formula (y - y1) = m(x - x1) and find the required equation.
We can plug in m value and (x1, y1) value and find the equation.
y - (-4) = 6/5(x - (-6))
y + 4 = 6/5(x + 6)
Using the distributive property a(b + c) = ab + ac, we get
y + 4 = 6/5 x + 36/5
y = 6/5 x + 36/5 - 4
y =6/5 x +(
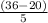
y =