Question

Graph the system of quadratic Inequalities.(please show work on how to find the points to graph)

Answer 1

Consider the set of inequalities as,

`\begin{gathered} y\ge2x^2+x-5\ldots(1) \\ y<-x^2+5x+10\ldots(2) \end{gathered}`

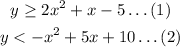
Factorize the first inequality using the quadratic formula as follows,

`\begin{gathered} y\ge(x-\frac{-1\pm\sqrt[]{1^2-4(2)(-5)}}{2(2)}) \\ y\ge(x-\frac{-1\pm\sqrt[]{1+40}}{4}) \\ y\ge(x-\frac{-1\pm\sqrt[]{41}}{4}) \\ y\ge(x-\frac{-1+\sqrt[]{41}}{4})(x-\frac{-1-\sqrt[]{41}}{4}) \\ y\ge(x+\frac{1-\sqrt[]{41}}{4})(x+\frac{1+\sqrt[]{41}}{4}) \end{gathered}`

Now, consider that the origin lies inside the parabola,

`\begin{gathered} 0\ge(0+\frac{1-\sqrt[]{41}}{4})(0+\frac{1+\sqrt[]{41}}{4}) \\ 0\ge(\frac{1-\sqrt[]{41}}{4})(\frac{1+\sqrt[]{41}}{4}) \\ 0\ge(1)/(16)(1-\sqrt[]{41})(1+\sqrt[]{41}) \\ 0\ge(1)/(16)(1^2-\sqrt[]{41}^2) \\ 0\ge(1)/(16)(1-41) \\ 0\ge(-40)/(16) \end{gathered}`

As the point insider the parabola satisfies the inequality, it can be concluded that all points lying inside this parabola will be the solution of the inequality.

Now, factorize the other inequality,

`\begin{gathered} y<-x^2+5x+10 \\ y<-(x^2-5x-10) \\ y<-(x-\frac{5\pm\sqrt[]{5^2-4(1)(-10)}}{2(-1)}) \\ y<-(x-\frac{5\pm\sqrt[]{25+40}}{2}) \\ y<-(x-\frac{5\pm\sqrt[]{65}}{2}) \\ y<-(x-\frac{5+\sqrt[]{65}}{2})(x-\frac{5-\sqrt[]{65}}{2}) \end{gathered}`

Again, the origin lies inside the parabola.

Check if the origin satisfied the inequality,

`\begin{gathered} 0<-(0-\frac{5+\sqrt[]{65}}{2})(0-\frac{5-\sqrt[]{65}}{2}) \\ 0<-(-\frac{5+\sqrt[]{65}}{2})(-\frac{5-\sqrt[]{65}}{2}) \\ 0<(-1)/(4)(5+\sqrt[]{65})(5-\sqrt[]{65}) \\ 0<(-1)/(4)(5^2-\sqrt[]{65}^2) \\ 0<(-1)/(4)(25-65) \\ 0<10 \end{gathered}`

Since the origin satisfies the inequality, it can be concluded that the region lying inside the parabola will be the solution region for the inequality.

The following diagram represents the solution region to both the inequalities and the solution of the system of inequalities is given by the common region shared by both the inequalities,

Here, the red colour is assigned to the first inequality and the blue colour is assigned to the second inequality.