Question

19. The equation 7( − 11)^2 + 7( + 13)^2 = 343 is.a. A circle of radius 49 centered on (11,-13)b. A circle of radius 7 centered on (-11,-13)c. A circle of radius 7 centered on (11,-13)d. A circle of radius 343 centered on (11,-13)e. A circle of radius 49 centered on (-11,13)

Answer 1

Circle equation

The equation of the circle looks like:

`(x-a)^2+(y-b)^2=r^2`

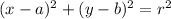
where a, b and r are numbers.

The principal parts of the circle are its center and its radius:

(a, b) is the location of the center

r is the radius

We have the equation:

`7(x-11)^2+7(y+13)^2=343`

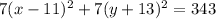
and we want to convert it into another aquation that looks like the circle formula. We want to remove the 7 outside the parenthesis. We do this by factoring it:

`\begin{gathered} 7(x-11)^2+7(y+13)^2 \\ =7\lbrack(x-11)^2+(y+13)^2\rbrack \\ \downarrow \\ 7\lbrack(x-11)^2+(y+13)^2\rbrack=343 \end{gathered}`

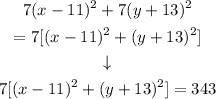
Now, we can take the 7 to the right side:

`\begin{gathered} 7\lbrack(x-11)^2+(y+13)^2\rbrack=343 \\ \downarrow\text{ taking 7 to the right} \\ (x-11)^2+(y+13)^2=(343)/(7)=49 \end{gathered}`

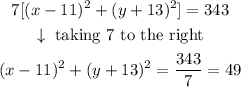
Then,

`\begin{gathered} (x-11)^2+(y+13)^2=49 \\ \downarrow\text{ since }7^2=49 \\ (x-11)^2+(y+13)^2=7^2 \\ \downarrow\text{ since +}13=-(-13) \\ (x-11)^2+(y-(-13))^2=7^2 \end{gathered}`

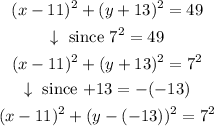
Now we have an equation that look like the original equation of the circle:

`\begin{gathered} (x-a)^2+(y-b)^2=r^2 \\ \uparrow\downarrow \\ (x-11)^2+(y-(-13))^2=7^2 \end{gathered}`

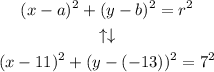
Comparing them, we have that:

a = 11

b = -13

and

r = 7

This means that this is a circle centered on

(a, b) = (11, -13)

and that has a radius of 7.

ANSWER: c. A circle of radius 7 centered on (11,-13).