Question

A ray of monochromatic light ( f = 5.09 × 10^14 Hz) passes from air into Lucite at an angle

of incidence of 30.˚.

Using a protractor and straightedge, on the diagram, draw the refracted ray in the
Lucite.

Answer 1

Let us consider the air with the index 1 and the lucite with index 2. Using the Snell's Secound Law, we have:


`(sen\O_(2))/(sen\O_(1)) = (n_(2))/(n_(1)) \\ sen\O_(2)= (n_(2)*sen\O_(1))/(n_(1))`

Entering the unknowns, remembering that the air refrective index is 1 and the lucite refrective index is 1.5, comes:


`sen\O_(2)= (n_(2)*sen\O_(1))/(n_(1)) \\ sen\O_(2)= (1.5* (1)/(2) )/(1) \\ sen\O_(2)=0.75`

Using the arcsin properties, we get:


`sen\O_(2)=0.75 \\ arcsin(0.75)=\O_(2) \\ \boxed {\O_(2)=48.59^o}`

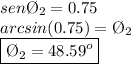
Obs: Approximate results, and the drawing is attached

If you notice any mistake in my english, let me know, because i am not native.