Question

I'm helping my son with his algebra (attempting to anyway).  We've got a problem that I can't quite understand... Simplify the equation (3x^-3)^2(-2xy).  I

Answer 1

`(3x^(-3))^2(-2xy)}`

The square (²) can be distributed to each factor inside those parentheses.
3² = 3 × 3 = 9
as for the x^-3, we want to multiply our exponents together, leaving x^-6.


`(9x^(-6))(-2xy)`

Note that since multiplication is commutative/associative, we can multiply these together in whatever order to simplify.

The x on the right can be rewritten as x¹. Multiply that and x^-6 together to get x^-5. (we just add the exponents)
As for the 9 and -2, multiply those together to get -18.

Now we have
`-18x^(-5)y`.

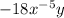
Lastly, if you don't want a negative exponent in your answer:
It can be flipped to the bottom because of this property:


`x^(-n)=(1)/(x^n)`

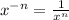
This leaves us with
`\boxed{(-18y)/(x^5)}`