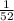Question

You draw one card from a 52-card deck. Then the card is replaced in the deck and the deck isshuffled, and you draw again. Find the probability of drawing a nine the first time and a diamond thesecond time.The probability of drawing a nine the first time and a diamond the second time is(Type an integer or a simplified fraction.)

Answer 1

GIVEN:

You draw one card from a 52-card deck. Then the card is replaced in the deck and the deck is shuffled, and you draw again.

Required;

Find the probability of drawing a nine the first time and a diamond the

second time.

Step-by-step solution;

To solve this math problem, we take note of the following;

A standard 52-card deck contains,

`\begin{gathered} 13\text{ }Hearts \\ \\ 13\text{ }Diamonds \\ \\ 13\text{ }Clubs \\ \\ 13\text{ }Spades \end{gathered}`

Each of the suits (that is, hearts, diamonds, clubs and spades) has a 9 card each which means there are four 9s in the entire 52-card deck.

Hence, the probabilty of drawing a 9 is given as follows;

`\begin{gathered} Probability\text{ }of\text{ }[event]=\frac{number\text{ }of\text{ }required\text{ }outcomes\text{ }}{number\text{ }of\text{ }all\text{ }possible\text{ }outcomes} \\ \\ Probability\text{ }[9]=(4)/(52) \\ \\ Probability\text{ }[9]=(1)/(13) \end{gathered}`

Note that the card is replaced before the commencement of the next experiment.

This means for the second draw, we have a complete 52-card deck.

Therefore, for the probability of drawing a diamond, note that we have 13 diamonds in all. Hence,

`\begin{gathered} Probability\text{ }[diamond]=(13)/(52) \\ \\ Probability\text{ }[diamond]=(1)/(4) \end{gathered}`

The probability of event A and event B is the product of probabilities. This means;

`Probability\text{ }of\text{ }A\text{ }and\text{ }Probability\text{ }of\text{ }B=P[A]\text{ }*\text{ }P[B]`

Therefore, the probability of drawing a nine the first time and a diamond the second time is given as;

`\begin{gathered} P[9]\text{ }and\text{ }P[diamond]=(1)/(13)*(1)/(4) \\ \\ P[9]\text{ }and\text{ }P[diamond]=(1)/(52) \end{gathered}`

ANSWER:

`(1)/(52)`