Question

If 1900 square centimeters of material are available to make a box with a square base and an open top, find the largest possible volume of the box.

Answer 1

Volume =
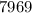`7969` cubic centimeter

Explanation:

Let the length of each side of the base of the box be A and the height of the box be H.

Area of material required to make the box is equal to is
`A^2 + 4*A*H.`

`A^2 + 4*A*H = 1900`

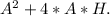
Rearranging the above equation, we get -

``H = ((1900 - A^2))/((4*A))`

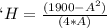
Volume of box is equal to product of base area of box and the height of the box -

`V = A*A* H`

Substituting the given area we get -

`(A^2*(1900 - A^2))/(4A) = ((1900*A - A^3))/(4)`

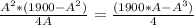
For maximum volume

`(dV)/(dA) =0`

`( 1900)/(4) - (3*A^2)/(4) = 0`

`A^2 = (1900)/(3)`

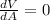
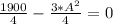
Volume of the box

=
`\frac{(1900)/(3)*(1900 - (1900)/(3)) }{4 * \sqrt{(1900)/(3) } }`

=
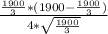
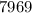`7969` cubic centimeter