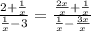Question

How do you find a common denominator for a function Explain how to pass from step 2 to step 3

Answer 1

To find the common denominator, we need to multiply each fraction by the denominator of the other fraction. For example, for

`2+(1)/(x)=(2)/(1)+(1)/(x)`

When need to multiply the first fraction by x and the second fraction by 1 as follows

`(2\cdot x)/(1\cdot x)+(1\cdot1)/(x\cdot1)=(2x)/(x)+(1)/(x)`

Therefore, the numerator of the function is changed from 2 + 1/x to 2x/x + 1/x

In the same way, we can transform the denominator of the function as follows:

`(1)/(x)-3=(1)/(x)-(3)/(1)=(1\cdot1)/(x\cdot1)-(3\cdot x)/(1\cdot x)=(1)/(x)-(3x)/(x)`

So, from step 2 to step 3, they change 2 + 1/x to 2x/x + 1/x and change 1/x -3 by 1/x - 3x/3. This is

`(2+(1)/(x))/((1)/(x)-3)=((2x)/(x)+(1)/(x))/((1)/(x)-(3x)/(x))`