Since they are consecutive, meaning that one is another added to a unit.
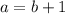
Where: a>b
Now, we must mathematizing the problem:

Note that, the result was expected because we made "a^2-b^2" in order to give a positive number, since "a" and "b" are positive, then the sum of both should also give a positive number.
If you notice any mistake in English, please let me know, because I'm not native.