Question

Can someone help me with this?
thanks in advance ʕ•ᴥ•ʔ

Answer 1

A)

Firtly, we edd to simplify the plots.


`3.9^x-5.6^x+2.4^x\ \textless \ 0 \\ (3.3^(2x)-5.2^x.3^x+2.2^(2x))/(2^x.3^x) \ \textless \ 0 \\3.((3)/(2))^x -5+2. ((3)/(2))^(-x)\ \textless \ 0 \\ 3.((3)/(2))^x+ (2)/(((3)/(2))^x) \ \textless \ 5`

`3.((3)/(2))^(2x)+ 2 \ \textless \ 5.((3)/(2))^x \\ 3.(((3)/(2))^x)^2-5.((3)/(2))^(x)+2\ \textless \ 0`

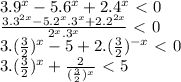
Making the substitution and equting to zero, we have:


`((3)/(2))^x=y`

`\\ \\ 3y^2-5y+2=0 \\ \\ \Delta=(-5)^2-4.3.2 \\ \Delta=25-25 \\ \Delta=1 \\ \\`

`x_(1)= (5+1)/(2.3) \\ x_(1)=1 \\ \\ x_(2)= (5-1)/(2.3) \\ x_(2)= (2)/(3)`

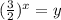
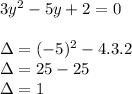
The result should be less than zero, soon:


`\boxed {S=(xeR/1\ \textless \ x\ \textless \ (2)/(3) )}`


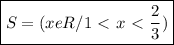
B)

Simply eliminating the logarithm, however, since the base is less than 1, we must reverse the inequality.


`log_{_(0.3)}(2x+3) \leq log_{_(0.3)}(x-1) \\ 2x+3 \geq x-1 \\ x \geq -4 \\ \\ \boxed x \geq -4)`

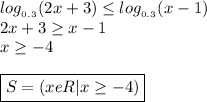
If you notice any mistake in my English, please know me, because I am not native.