Question

What is the solution set to the following system?x + y = 3x^2 = y^2 = 9

Answer 1

`\begin{cases}x+y=3 \\ x^2+y^2=9\end{cases}`

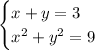
To solve the given system of equations:

1. Solve x in the first equation:

`\begin{gathered} x+y-y=3-y \\ \\ x=3-y \end{gathered}`

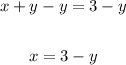
2. Use the value of x=3-y in the second equation:

`(3-y)^2+y^2=9`

3. Solve y:

`\begin{gathered} (a-b)^2=a^2-2ab+b^2 \\ \\ 3^2-2(3)(y)+y^2+y^2=9 \\ 9-6y+2y^2=9 \\ \\ 2y^2-6y=0 \\ 2y(y-3)=0 \\ \\ \end{gathered}`

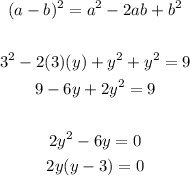
When the product of two factors is equal to zero, then you equal each factor to zero to find the solutions of the variable:

`\begin{gathered} 2y=0 \\ y=(0)/(2) \\ y=0 \\ \\ y-3=0 \\ y-3+3=0+3 \\ y=3 \end{gathered}`

Then, the solutions for variable y in the given system are:

y=0

y=3

4. Use the values of y to find the corresponding values of x:

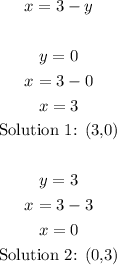
`\begin{gathered} x=3-y \\ \\ y=0 \\ x=3-0 \\ x=3 \\ \text{Solution 1: (3,0)} \\ \\ y=3 \\ x=3-3 \\ x=0 \\ \text{Solution 2: (0,3)} \end{gathered}`Then, the solutions for the given system of equations are: (3,0) and (0,3)quations

4. Use the values of y to find the corresponding values of x:

4. Use the values of y to find the corresponding values of x: