Question

Two straight lines have equations y = px + 4 and py = qx - 7 where p and q are constants. The two lines meet at the point (3,1). What is the value of q?

Answer 1

Given:

Equations of two lines are

`y=px+4`

`py=qx-7`

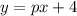
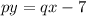
where, p and q are constants.

The two lines meet at the point (3,1).

To find:

The value of q.

Solution:

We have,

`y=px+4` ...(i)

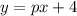`py=qx-7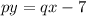` ...(ii)

The two lines meet at the point (3,1). It means both equations must be satisfied by the point (3,1).

Putting x=3 and y=1 in (i), we get

`1=p(3)+4`

`1-4=3p`

`(-3)/(3)=p`

`-1=p`

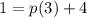
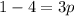
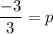
The value of p is -1.

Now, putting p=-1, x=3 and y=1 in (ii), we get

`(-1)(1)=q(3)-7`

`-1+7=3q`

`(6)/(3)=q`

`2=q`

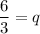
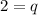
Therefore, the value of q is 2.