√(x^2+3x+4) + √(x+1) \ \textgreater \ 1,4

Question

`√(x^2+3x+4) + √(x+1) \ \textgreater \ 1,4`

Answer 1

First we must pay attention to the existence conditions.


`\left \{ {{(I) x^2+3x+4 \geq 0 -\ \textgreater \ x \geq -1.5} \atop {(II)x+1 \geq 0-\ \textgreater \ x \geq -1}} \right. \\ \\ \boxed {E.C: x \geq -1}`

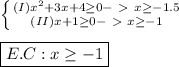
Now we can proceed with calculations.


`√((x+1.5)^2)+ √(x+1)\ \textgreater \ 1.4 \\ √(x+1)\ \textgreater \ 1.4-x-1.5 \\ ( √(x+1))^2\ \textgreater \ (-x-0.1)^2 \\ x+1\ \textgreater \ x^2+0.2x+0.01 \\ x^2-0.8x-0.99\ \textless \ 0`


`\Delta = (-0.8)^2-4.1.(-0.99) \\ \Delta = 0.64+3.96 \\ \Delta =4.6 \\ \\ x_(1)= (0.8+ √(4.6) )/(2) \\ \\ x_(2)= (0.8- √(4.6) )/(2)`

Note that the second root no satisfies the existence condition, then it should not be in solution.


`\boxed { S=(0.8+ √(4.6))/(2) }`

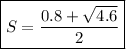
If you notice any mistake in English, please let me know, because I'm not native.