Given:
The trinomial is
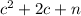
To find:
The value of n for which the given trinomial is a perfect square and then factor the trinomial.
Solution:
We know that, the perfect square trinomial is given by
 ...(i)
...(i)
We have,
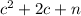 ...(ii)
...(ii)
From (i) and (ii), we get
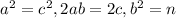

Similarly,
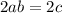
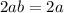
![[\because a=c]](https://img.qammunity.org/2022/formulas/mathematics/college/ejxl640urg0x1qbpcihpq020w4sboclhu6.png)
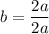
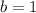
Now,
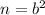
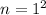
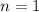
The value of n is 1.
The trinomial is
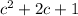
Splitting the middle term, we get
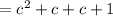
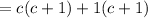
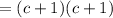
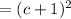
Therefore, the factorized form of the trinomial is
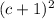 .
.