3(x - 2) = 22 - x
First, we will need to expand the problem. 3(x - 2) will turn into 3x - 6 = 22 - x, but to the fact of multiplying 3 times 2.

Second, we can start doing everything on one side of the problem. Let's add 6 to each side.
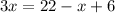
Third, we can now simplify the right part of the problem. 2x = 22 - x + 6. Ignore the '2x =', and focus on 22 - x + 6. To solve this, the variable (x) is considered the number one. But, in this case, ignore the variable as well so that it looks like 22 + 6. In the end, you'll add on your variable.
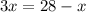
Fourth, we can now add the variable (x) to each side. Again, a variable by itself can also be shown as one.
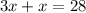
Fifth, we can now simplify 3x + x. Again, with the variable being considered 1, we can now look at the problem as 3x + 1. Basically, add 3 + 1 and add the variable onto that.
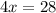
Sixth, we can divide each side by 4 now. This will create a fraction which we will simplify to get our answer.
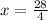
Seventh, our last step is to simplify the fraction. To do this, we can ask ourselves, what multiples with 4 to equal 28? 28 ÷ 4 = 7. So, this equation only has
one solution.
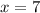
Answer:
