eGiven:
The mass of the crate is,
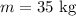
The coefficient of friction between the floor and the crate is,
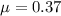
The force applied by the man is ,
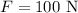
The frictional force on the crate is,

Here the applied force is less than the frictional force. so the crate will not move.
part b
if the other person applies force,

WE CAN WRITE the vertical force,
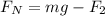
the frictional force is then,
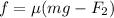
we can say,
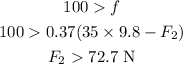
part c
the maximum frictional force is as calculated above,
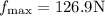
the extra force by the other person if added we can write,

hence the added force in26.9 N