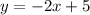We are asked to find the equation of the line that has the same slope as the equation below
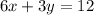
And it passes through the point (2, 1)
Let us first re-write the given equation into the slope-intercept form.
To do that, simply separate out the y variable.
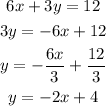
The standard slope-intercept form is given by
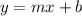
Where m is the slope and b is the y-intercept.
Comparing the standard form with the above equation we see that
Slope = m = -2
So, the equation of the line that we want to find out becomes
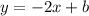
Now we need to find out the value of y-intercept (b)
Since it is given that the line passes through the point (2, 1) so we can substitute it into the above equation and solve for b.
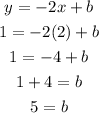
So, the value of the y-intercept is 5
Therefore, the equation of the line is