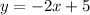Question

what is the equation of the line that has the same slope as the equation 6X + 3y equals 12 and passes through the point 2 and 1

Answer 1

We are asked to find the equation of the line that has the same slope as the equation below

`6x+3y=12`

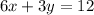
And it passes through the point (2, 1)

Let us first re-write the given equation into the slope-intercept form.

To do that, simply separate out the y variable.

`\begin{gathered} 6x+3y=12 \\ 3y=-6x+12 \\ y=-(6x)/(3)+(12)/(3) \\ y=-2x+4 \end{gathered}`

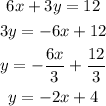
The standard slope-intercept form is given by

`y=mx+b`

Where m is the slope and b is the y-intercept.

Comparing the standard form with the above equation we see that

Slope = m = -2

So, the equation of the line that we want to find out becomes

`y=-2x+b`

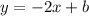
Now we need to find out the value of y-intercept (b)

Since it is given that the line passes through the point (2, 1) so we can substitute it into the above equation and solve for b.

`\begin{gathered} y=-2x+b \\ 1=-2(2)+b \\ 1=-4+b \\ 1+4=b \\ 5=b \end{gathered}`

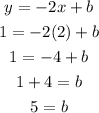
So, the value of the y-intercept is 5

Therefore, the equation of the line is

`y=-2x+5`