Question

hexagon is equal to the area of an equilateral triangle whose perimeter is 36 inches. Find the length of a side of the regular hexagon.

Answer 1

`Perimter\ of\ equilateral\ triangle\ =36\\ a- \ side\ of\ triangle\\ 36=3a\ |:3\\ a=12\\\\ Area\ of\ equilateral\ triangle:\\ A=(a^2√(3))/(4)\\ A=(12^2√(3))/(4)\\ A=(144√(3))/(4)=36\sqrt3 \\\\ Hegagon\ can\ be\ divided\ into\ 6\ equilateral\ small\ triangles.\\Area\ of\ one\ of\ them: A_s=(A)/(6)=(36\sqrt3)/(6)=6√(3)\\ s-side\ of\ equilateral\ =\ side\ of\ small\ triangle\\ A_s=(s^2√(3))/(4)=6√(3)\ |*4 \\ s^2\sqrt3=24\sqrt3\ |\sqrt3\\ s^2=24\\ s=√(24)`
`√(24)=√(4*6)=2\sqrt6\\\\ Side\ of\ hexagon\ equals\ 2\sqrt6\ inches`

Answer 2

`2√(6)`

Explanation:

Perimeter of equilateral triangle = 36 inches

Formula of perimeter of equilateral triangle =
`3* side`

⇒
`36=3* side`

⇒
`(36)/(3) = side`

⇒
`12= side`

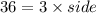
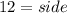
Thus each side of equilateral triangle is 12 inches

Formula of area of equilateral triangle =
`(√(3))/(4) a^(2)`

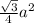
Where a is the side .

So, area of the given equilateral triangle =
`(√(3))/(4) * 12^(2)`

=
`36√(3)`

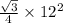
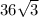
Since hexagon can be divided into six small equilateral triangle .

So, area of each small equilateral triangle =
`(36√(3))/(6)`

=
`6√(3)`

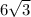
So, The area of small equilateral triangle :

`(√(3))/(4)a^(2) =6√(3)`

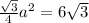
Where a is the side of hexagon .

`(1)/(4)a^(2) =6`

`a^(2) =6* 4`

`a^(2) =24`

`a =√(24)`

`a =2√(6)`

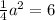
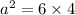
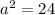
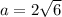
Hence the length of a side of the regular hexagon is
`2√(6)`