Question

The force of gravity between the Sun and Jupiter is 5

Answer 1

1.8 x 10²⁷ kg

Step-by-step explanation

Given:

• The force of gravity between the Sun and Jupiter, F = 5x10²³N

,

• The mass of the Sun, m₁ = 2x10³⁰kg

,

• The distance between Jupiter and the Sun, r = 7x10¹¹m

Unknown:

• The mass of Jupiter, m₂

By Newton's Law of Universal Gravitation,

`F=G\cdot(m_1m_2)/(r^2)`

Where G is the gravitational constant, which has a value of approximately 6.67x10⁻¹¹m³/kg*s².

Solving this equation for m2,

`m_2=(r^2\cdot F)/(G\cdot m_1)`

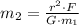
Replace with the values and solve,

Hence, the mass of Jupiter is 1.8x 10²⁷ kg.