This is a permutation problem.
The expression n permutation r is expressed as:
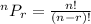
In like manner, n permutation 4 will be:
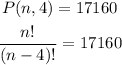
Evaluation the permutation operation above, we have:
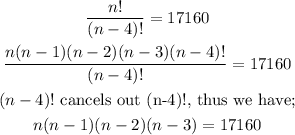
Expanding the Left hand side of the equation; we have:
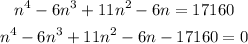
By factorization, the equation becomes;
![\begin{gathered} \mleft(n+10\mright)\mleft(n-13\mright)\mleft(n^2-3n+132\mright)=0 \\ (n^2-3n+132)\text{ is not factorizable and would also produce unreal roots, thus the value of n from the expression can't be correct} \\ n+10=0\text{ will produce n=-10, we can have a negative result for permutation problems} \\ \text{Thus, the correct answer is;} \\ n-13=0 \\ n=13 \end{gathered}]()
Hence, the value of n is 13, option C