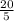Solution:
Let the denominator be represented by a
The numerator of a certain fraction is four times the denominator
Then, the numerator will be 4a
The original fraction is
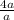
If 10 is added to both the numerator and the denominator, as shown below
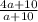
The resulting fraction is equivalent to 2, i.e.

Solve for a
Crossmultiply
![\begin{gathered} 4a+10=2(a+10) \\ Open\text{ the brackets on the right side of the equation} \\ 4a+10=2a+20 \\ Collect\text{ like terms} \\ 4a-2a=20-10 \\ 2a=10 \\ Divide\text{ both sides by 2} \\ (2a)/(2)=(10)/(2) \\ a=5 \end{gathered}]()
Where a = 5,
The original fraction is
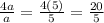
Hence, the original fraction is