Question

1. The monthly revenue from selling x units of a certaincommodity is given to beR(x) = 12x - 0.01x2dollars. Determine the number ofunits that must be sold each month maximize the revenue. What is the correspondingmaximum revenue?

Answer 1

Monthly revenue:

`R(x)=12x-0.01x^2`

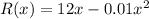
As the monthly revenue is given by a quadratic equation, the number of units that must be sold each month maximize the revenue and the maximum revenue are the coordinates of the vertex for the parabola that correspond to the given function.

x is the number of units

y is the maximum revenue

To find the x coordinate of the vertex, use the next formula:

`\begin{gathered} f(x)=ax^2+bx+c \\ \\ x=-(b)/(2a) \\ \\ \\ x=-(12)/(2(-0.01))=-(12)/(-0.02)=600 \end{gathered}`

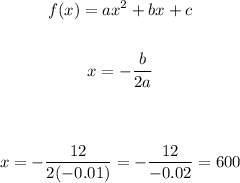
Use the x-coordinate in the function to find the y-coordinate (R(600)):

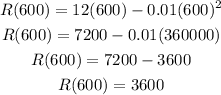
`\begin{gathered} R(600)=12(600)-0.01(600)^2 \\ R(600)=7200-0.01(360000) \\ R(600)=7200-3600 \\ R(600)=3600 \end{gathered}`Then, the number of units that must be sold each month to maximize the revenue is 600 and the maximum revenue is $3,600