Question

The volume of a cylinder is 90π cm^3. If the radius is 3 cm, what is the heightof the cylinder?3 cmO A. 30 cmOB. 15 cmO C. 5 cmD. 10 cm

Answer 1

Given:

Volume of cylinder, V = 90π cm³

Radius, r = 3 cm

Let's find the height of the cylinder.

To find the height, given the volume, apply the formula for the volume of a cylinder:

`V=\pi r^2h`

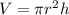
Where h is the height.

Let's rewrite the formula for h to solve for h.

Re-arrange the equation:

`\pi r^2h=V`

Divide both sides by πr²:

`\begin{gathered} (\pi r^2h)/(\pi r^2)=(V)/(\pi r^2) \\ \\ h=(V)/(\pi r^(2)) \end{gathered}`

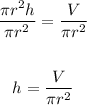
Now, substitute values into the equation and solve for h.

Where:

V = 90π

r = 3

We have:

`\begin{gathered} h=(90\pi)/(\pi(3)^2) \\ \\ h=(90\pi)/(9\pi) \\ \\ h=(10\pi)/(\pi) \\ \\ h=10\text{ cm} \end{gathered}`

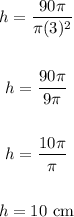
Therefore, the height of the cylinder is 10 cm.

ANSWER:

D. 10 cm