Question

Determine whether the information in each table is linear. If so find the constant rate of change. If not explain your reasoning..

Answer 1

Step-by-step explanation

Since we have the table with the values of x and y, we can draw the graph as show as follows:

The rate of change can be computed by taking two given points and calculating the slope as shown as follows:

`\text{Slope}=(y_2-y_1)/(x_2-x_1)`

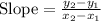
As we have (x_1,y_1) = (1,13) and (x_2,y_2) = (3,39), substituting terms:

`\text{Slope}=(39-13)/(3-1)`

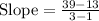
Subtracting numbers:

`Slope=(26)/(2)`

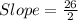
Simplifying:

`\text{Slope}=rate_{\text{ }}of_{\text{ }}change=13`

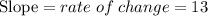
The constant rate of change is 13

The function is linear because we have a constant rate of change and the form of the graph is a line.