Question

What is the angular speed and the number of revolutions per minute?

Answer 1

Given data:

* The linear speed of the cyclist is v = 19 miles per hour.

* The diameter of the circular motion is d = 30 inches.

Solution:

The radius of the circular motion is,

`\begin{gathered} r=(d)/(2) \\ r=(30)/(2) \\ r=15\text{ inches} \end{gathered}`

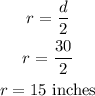
The radius of the circular path in terms of feet is,

`\begin{gathered} r=(15)/(12)\text{ ft} \\ r=1.25\text{ ft} \end{gathered}`

The linear velocity of the cyclist in terms of feet per minute is,

`\begin{gathered} v=19*(5280)/(60)\text{ ft/min} \\ v=19*(5280)/(60)\text{ ft/min} \\ v=1672\text{ ft/min} \end{gathered}`

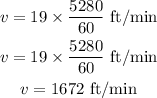
The angular speed of the cyclist is,

`\begin{gathered} v=r\omega \\ \omega=(v)/(r) \end{gathered}`

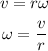
Substituting the known values,

`\begin{gathered} \omega=(1672)/(1.25) \\ \omega=1337.6\text{ rad/min} \\ \omega=1338\text{ rad/min} \end{gathered}`

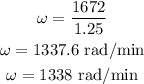
Thus, the angular speed of the cyclist is 1338 radian per minute.

(b). The number of revolutions in one minute is,

`\begin{gathered} \omega=2\pi f \\ f=(\omega)/(2\pi) \end{gathered}`

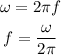
Substituting the known values,

`\begin{gathered} f=(1338)/(2\pi) \\ f=213\text{ rev/min} \end{gathered}`

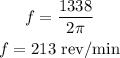
Thus, the number of revolutions per minute is 213 rev/min.