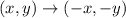Question

How to write the rule for #14. if there is no rule, describe the transformation in words.

Answer 1

Given the Pre-Image (the original figure) JKL, and the Image (the figure after the transformation) J'K'L', you can identify that the vertices of JKL are:

`\begin{gathered} J(-2,-4) \\ K(-2,-2) \\ L(1,-2) \end{gathered}`

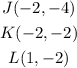
And the vertices of the Image are:

`\begin{gathered} J^(\prime)(4,2) \\ K^(\prime)(2,2) \\ L^(\prime)(-1,2) \end{gathered}`

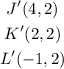
You can notice that the signs of the coordinates of the Image are obtained by multiplying the original coordinates by -1.

By definition, the rule for a Rotation of 180 degrees centered at the Origin is:

`(x,y)\rightarrow(-x,-y)`

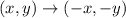
Hence, the answer is:

`(x,y)\rightarrow(-x,-y)`