Question

The total cost (in dollars) of producing x a golf clubs per day is given by the formula C(x) = 550 + 130x - 0.9x^2(A) Find the marginal cost at a production level of r golf clubs.C'(x) =(B) Find the marginal cost of producing 55 golf clubs.Marginal cost for 55 clubs

Answer 1

We have a cost function that express the cost of producing x golf clubs per day:

`C(x)=550+130x-0.9x^2`

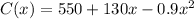
A) We have to to find the marginal cost. The marginal cost at a certain level of production x represents the cost of producing one more unit.

It can be calculated as the first derivative of the cost function:

`\begin{gathered} C^(\prime)(x)=550(0)+130(1)-0.9(2x) \\ C^(\prime)(x)=130-1.8x \end{gathered}`

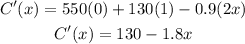
B) In this case, we have to calculate the marginal cost when the level of production is 55 golf clubs (x = 55):

`\begin{gathered} C^(\prime)(55)=130-1.8(55) \\ C^(\prime)(55)=130-99 \\ C^(\prime)(55)=31 \end{gathered}`

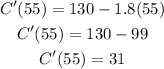
Answer:

A) C'(x) = 130 - 1.8x

B) C'(55) = 31