Question

Suppose Y varies directly as X, and y = 9 when x = 3/2. Find y when x = 1.

Answer 1

to vary directly is to be in proportion

y/x = y/x

9/(3/2) = y
9(2/3) = y
y = 6

Answer 2

Answer: The required value of y is 6.

Step-by-step explanation: We are given that y varies directly as x and y = 9 when
`x=(3)/(2).`

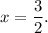
We are to find the value of y when x = 1.

According to the given information, we have

`y\propto x\\\\\Rightarrow y=k* x~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[\textup{where k is the constant of integration}]\\\\\Rightarrow y=kx~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

When y = 9 and
`x=(3)/(2),` we have from equation (i) that

`9=k*(3)/(2)\\\\\\\Rightarrow k=(18)/(3)\\\\\Rightarrow k=6.`

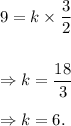
So, equation (i) becomes

`y=6x.`

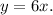
Therefore, when x = 1, we get

`y=6*1=6.`

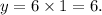
Thus, the required value of y is 6.