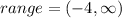Question

Given f (x) = x^2 + 2x – 6 and values of the linear function g(x) in the table, what is the range of (f + g)(x)?

Answer 1

Given:

`f(x)=x^2+2x-6`

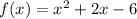
We get two points from the given table.

(-6,14) and (-3,8).

Required:

We need to find the range of (f+g)(x).

Step-by-step explanation:

Consider the equation of the linear function.

`g(x)=mx+b`

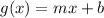
where m is the slope.

Consider the formula to find the slope.

`m=(y_2-y_1)/(x_2-x_1)`
`Substitute\text{ }y_2=8,y_1=14,x_2=-3,\text{ and }x_1=-6\text{ in the formula to find the slope m.}`

`m=(8-14)/(-3-(-6))`

`m=(-6)/(3)=-2`

`Substitute\text{ m=-3 in the equation }g(x)=mx+b.`
`g(x)=-2x+b`
`Substitute\text{ x=-6 and g\lparen-6\rparen=14 in the equation to find the value of b.}`

`14=-2(-6)+b`

`14=12+b`

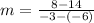
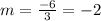
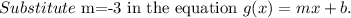
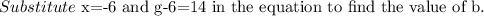
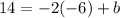
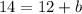
Subtract 12 from both sides of the equation.

`14-12=12-12+b`

`2=b`

`Substitute\text{ b =2 in the equation }g(x)=-2x+b.`
`g(x)=-2x+2`

`We\text{ know that }(f+g)(x)=f(x)+g(x).`
`Substitute\text{ }f(x)=x^2+2x-6\text{ and }g(x)=-2x+2\text{ in the equation.}`

`(f+g)(x)=(x^2+2x-6)+(-2x+2)`

`=x^2+2x-6-2x+2`

`=x^2+2x-2x-6+2`

`=x^2-4`
`\text{We get }(f+g)(x)=x^2-4.`

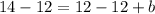
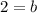
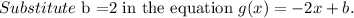
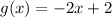
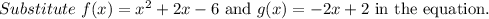
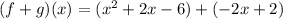
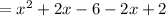
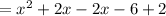
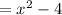
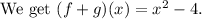
The graph of the function (f+g)(x).

We know that the range of a graph consists of all the output values shown on the y-axis.

The minimum value of the range is -4.

The graph moves upward to infinity.

The maximum value of the range is infinity.

`range=(-4,\infty)`

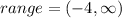
Final answer:

`range=(-4,\infty)`