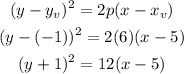1. Focus at (4 , 3), directriz= 2
Therefore, the vertex have coordinates (3 , 3 ) and p=2.
Where p is the distance between the focus and the vertex.
The equation of parabolas will be:
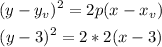
2. Focus at (2 , -1), directriz, x=8.
The vertex will be: (5 , -1) and p=6.
Replacing in the equation: