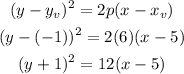Question

Part JTo practice writing the equations of horizontal parabolas, write the equations of these two parabolas in vertex form:focus at (4, 3), and directrix x = 2focus at (2, -1), and directrix x = 8

Answer 1

1. Focus at (4 , 3), directriz= 2

Therefore, the vertex have coordinates (3 , 3 ) and p=2.

Where p is the distance between the focus and the vertex.

The equation of parabolas will be:

`\begin{gathered} (y-y_v)^2=2p(x-x_v) \\ (y-3)^2=2*2(x-3) \end{gathered}`

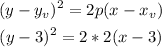
2. Focus at (2 , -1), directriz, x=8.

The vertex will be: (5 , -1) and p=6.

Replacing in the equation:

`\begin{gathered} (y-y_(v))^(2)=2p(x-x_(v)) \\ (y-(-1))^2=2(6)(x-5) \\ (y+1)^2=12(x-5) \end{gathered}`