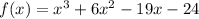Question

Which of the following is a polynomial function in standard form with zeros at –8, –1, and 3?

A) f(x) = (x + 8)(x + 1)(x – 3)
B) f(x) = x^3 – 6x^2 – 19x + 24
C) f(x) = x^3 + 6x^2 – 19x – 24
D) f(x) = (x – 8)(x – 1)(x + 3)

Answer 1

The answer is A because zeros of polynomial functions are found by setting each factor equal to zero and solving for x. The zeros of a function will be the opposite sign of the numbers inside each factor.

Answer 2

Option: C is the correct answer.

The polynomial in standard form is:

C)
`f(x)=x^3+6x^2-19x-24`

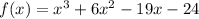
Explanation:

The standard form of a equation of a polynomial is written as :

We arrange the terms from least to highest power of x.

We know that if a polynomial has roots as:

a, b and c then the equation of the polynomial is given by:

`f(x)=(x-a)(x-b)(x-c)`

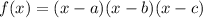
Here we have: a= -8 , b= -1 and c=3

Hence, the equation of the circle is given by:

`f(x)=(x-(-8))(x-(-1))(x-3)\\\\\\f(x)=(x+8)(x+1)(x-3)`

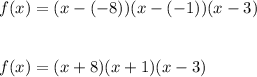
which on expanding gives:

`(x+8)(x+1)(x-3)=(x^2+9x+8)(x-3)\\\\(x+8)(x+1)(x-3)=x^3-3x^2+9x^2-27x+8x-24\\\\(x+8)(x+1)(x-3)=x^3+6x^2-19x-24`

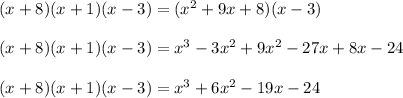
Hence, the standard equation of the polynomial is:

`f(x)=x^3+6x^2-19x-24`