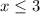2(4 + 2x) ≥ 5x + 5
First, we will need to expand our problem. Expanding is basically removing the parentheses. To do this, we will look at the first part of the problem to begin with. 2(4 + 2x). Since parentheses usually mean multiplication, we can start with 2(4). So, 2 × 4 = 8. We'll do the same thing with 2(2), 2 × 2 = 4.
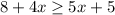
Second, our next step is to subtract 4 from each side. We are trying to get the variable (x) on one side of the problem by itself.
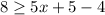
Third, we can now simplify (5x) + 5 - (4). I put parentheses around what we are going to focus on. Subtract 5x - 4 to get 1, which can be put as the variable (x). Now we have, x + 5.
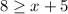
Fourth, let's subtract 5 from each side now. This will set up 8 - 5 which equals 3.
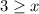
Fifth, we can switch sides now to get the result of this problem.
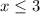
Answer: