Question

Solve the system of equations by elimination. 3x − y − z = 2 x + y + 2z = 4 2x − y + 3z = 9

Answer 1

Given:

The system of equations is,

`\begin{gathered} 3x-y-z=2.\text{ . .. . . .(1)} \\ x+y+2z=4\text{ . . . .. . (2)} \\ 2x-y+3z=9\text{ . . . . . . .(3)} \end{gathered}`

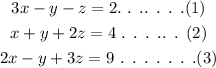
The objective is to solve the equations using the elimination method.

Step-by-step explanation:

Consider the equations (1) and (2).

`\begin{gathered} 3x-y-z=2 \\ (x+y+2z=4)/(4x+z=6) \\ \ldots\ldots\ldots.(4)\text{ } \end{gathered}`

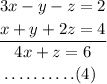
Now, consider the equations (2) and (3).

`\begin{gathered} x+y+2z=4 \\ (2x-y+3z=9)/(3x+5z=13) \\ \ldots\ldots\text{ . . . .. (5)} \end{gathered}`

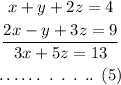
On multiplying the equation (4) with (-5),

`\begin{gathered} -5\lbrack4x+z=6\rbrack \\ -20x-5z=-30\text{ . . . . . .(6)} \end{gathered}`

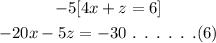
To find x :

On solving the equations (5) and (6),

`\begin{gathered} 3x+5z=13 \\ (-20x-5z=-30)/(-17x=-17) \\ x=(-17)/(-17) \\ x=1 \end{gathered}`

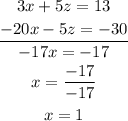
To find z :

Substitute the value of x in equation (6),

`\begin{gathered} -20(1)-5z=-30 \\ -5z=-30+20 \\ -5z=-10 \\ z=(-10)/(-5) \\ z=2 \end{gathered}`

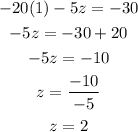
To find y :

Now, substitute the values of x and z in equation (2).

`\begin{gathered} x+y+2z=4 \\ 1+y+2(2)=4 \\ y=4-1-4 \\ y=-1 \end{gathered}`

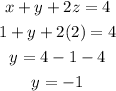
Hence, the value of x is 1, y is -1 and z is 2.